Basic Statistics: describing, modelling and reporting
Last updated on 2025-11-11 | Edit this page
Overview
Questions
- How can I detect the type of data I have?
- How can I make meaningful summaries of my data?
Objectives
- To be able to describe the different types of data
- To be able to do basic data exploration of a real dataset
- To be able to calculate descriptive statistics
- To be able to perform statistical inference on a dataset
Content
- Types of Data
- Exploring your dataset
- Descriptive Statistics
- Inferential Statistics
Data
R
# We will need these libraries and this data later.
library(tidyverse)
library(lubridate)
library(gapminder)
# create a binary membership variable for europe (for later examples)
gapminder <- gapminder %>%
mutate(european = continent == "Europe")
We are going to use the data from the gapminder package. We have added a variable European indicating if a country is in Europe.
The big picture
- Research often seeks to answer a question about a larger population by collecting data on a small sample
- Data collection:
- Many variables
- For each person/unit.
- This procedure, sampling, must be controlled so as to ensure representative data.
Descriptive and inferential statistics
Just as data in general are of different types - for example numeric vs text data - statistical data are assigned to different levels of measure. The level of measure determines how we can describe and model the data.
Describing data
- Continuous variables
- Discrete variables
How do we convey information on what your data looks like, using numbers or figures?
Describing continuous data.
First establish the distribution of the data. You can visualise this with a histogram.
R
ggplot(gapminder, aes(x = gdpPercap)) +
geom_histogram()
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
What is the distribution of this data?
What is the distribution of population?
The raw values are difficult to visualise, so we can take the log of the values and log those. Try this command
R
ggplot(data = gapminder, aes(log(pop))) +
geom_histogram()
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.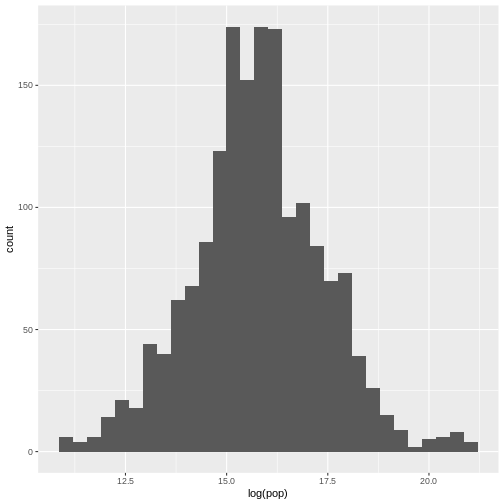
What is the distribution of this data?
Parametric vs non-parametric analysis
- Parametric analysis assumes that
- The data follows a known distribution
- It can be described using parameters
- Examples of distributions include, normal, Poisson, exponential.
- Non parametric data
- The data can’t be said to follow a known distribution
Describing parametric and non-parametric data
How do you use numbers to convey what your data looks like.
- Parametric data
- Use the parameters that describe the distribution.
- For a Gaussian (normal) distribution - use mean and standard deviation
- For a Poisson distribution - use average event rate
- etc.
- Non Parametric data
- Use the median (the middle number when they are ranked from lowest to highest) and the interquartile range (the number 75% of the way up the list when ranked minus the number 25% of the way)
- You can use the command
summary(data_frame_name)to get these numbers for each variable.
Mean versus standard deviation
- What does standard deviation mean?
- Both graphs have the same mean (center), but the second one has data which is more spread out.
R
# small standard deviation
dummy_1 <- rnorm(1000, mean = 10, sd = 0.5)
dummy_1 <- as.data.frame(dummy_1)
ggplot(dummy_1, aes(x = dummy_1)) +
geom_histogram()
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
R
# larger standard deviation
dummy_2 <- rnorm(1000, mean = 10, sd = 200)
dummy_2 <- as.data.frame(dummy_2)
ggplot(dummy_2, aes(x = dummy_2)) +
geom_histogram()
OUTPUT
`stat_bin()` using `bins = 30`. Pick better value `binwidth`.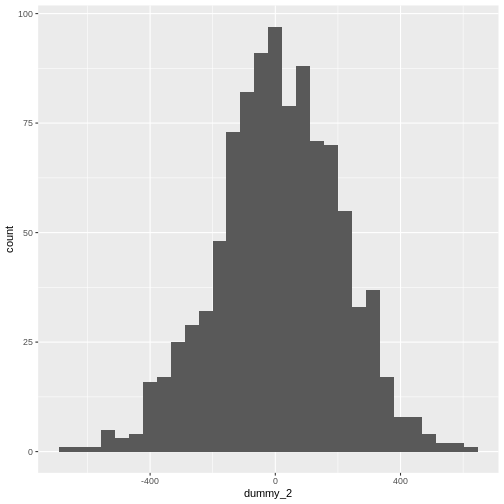
Calculating mean and standard deviation
R
mean(gapminder$pop, na.rm = TRUE)
OUTPUT
[1] 29601212Calculate the standard deviation and confirm that it is the square root of the variance:
R
sdpopulation <- sd(gapminder$pop, na.rm = TRUE)
print(sdpopulation)
OUTPUT
[1] 106157897R
varpopulation <- var(gapminder$pop, na.rm = TRUE)
print(varpopulation)
OUTPUT
[1] 1.12695e+16R
sqrt(varpopulation) == sdpopulation
OUTPUT
[1] TRUEThe na.rm argument tells R to ignore missing values in
the variable.
Describing discrete data
- Frequencies
R
table(gapminder$continent)
OUTPUT
Africa Americas Asia Europe Oceania
624 300 396 360 24 - Proportions
R
continenttable <- table(gapminder$continent)
prop.table(continenttable)
OUTPUT
Africa Americas Asia Europe Oceania
0.36619718 0.17605634 0.23239437 0.21126761 0.01408451 Contingency tables of frequencies can also be tabulated with table(). For example:
R
table(
gapminder$country[gapminder$year == 2007],
gapminder$continent[gapminder$year == 2007]
)
OUTPUT
Africa Americas Asia Europe Oceania
Afghanistan 0 0 1 0 0
Albania 0 0 0 1 0
Algeria 1 0 0 0 0
Angola 1 0 0 0 0
Argentina 0 1 0 0 0
Australia 0 0 0 0 1
Austria 0 0 0 1 0
Bahrain 0 0 1 0 0
Bangladesh 0 0 1 0 0
Belgium 0 0 0 1 0
Benin 1 0 0 0 0
Bolivia 0 1 0 0 0
Bosnia and Herzegovina 0 0 0 1 0
Botswana 1 0 0 0 0
Brazil 0 1 0 0 0
Bulgaria 0 0 0 1 0
Burkina Faso 1 0 0 0 0
Burundi 1 0 0 0 0
Cambodia 0 0 1 0 0
Cameroon 1 0 0 0 0
Canada 0 1 0 0 0
Central African Republic 1 0 0 0 0
Chad 1 0 0 0 0
Chile 0 1 0 0 0
China 0 0 1 0 0
Colombia 0 1 0 0 0
Comoros 1 0 0 0 0
Congo, Dem. Rep. 1 0 0 0 0
Congo, Rep. 1 0 0 0 0
Costa Rica 0 1 0 0 0
Cote d'Ivoire 1 0 0 0 0
Croatia 0 0 0 1 0
Cuba 0 1 0 0 0
Czech Republic 0 0 0 1 0
Denmark 0 0 0 1 0
Djibouti 1 0 0 0 0
Dominican Republic 0 1 0 0 0
Ecuador 0 1 0 0 0
Egypt 1 0 0 0 0
El Salvador 0 1 0 0 0
Equatorial Guinea 1 0 0 0 0
Eritrea 1 0 0 0 0
Ethiopia 1 0 0 0 0
Finland 0 0 0 1 0
France 0 0 0 1 0
Gabon 1 0 0 0 0
Gambia 1 0 0 0 0
Germany 0 0 0 1 0
Ghana 1 0 0 0 0
Greece 0 0 0 1 0
Guatemala 0 1 0 0 0
Guinea 1 0 0 0 0
Guinea-Bissau 1 0 0 0 0
Haiti 0 1 0 0 0
Honduras 0 1 0 0 0
Hong Kong, China 0 0 1 0 0
Hungary 0 0 0 1 0
Iceland 0 0 0 1 0
India 0 0 1 0 0
Indonesia 0 0 1 0 0
Iran 0 0 1 0 0
Iraq 0 0 1 0 0
Ireland 0 0 0 1 0
Israel 0 0 1 0 0
Italy 0 0 0 1 0
Jamaica 0 1 0 0 0
Japan 0 0 1 0 0
Jordan 0 0 1 0 0
Kenya 1 0 0 0 0
Korea, Dem. Rep. 0 0 1 0 0
Korea, Rep. 0 0 1 0 0
Kuwait 0 0 1 0 0
Lebanon 0 0 1 0 0
Lesotho 1 0 0 0 0
Liberia 1 0 0 0 0
Libya 1 0 0 0 0
Madagascar 1 0 0 0 0
Malawi 1 0 0 0 0
Malaysia 0 0 1 0 0
Mali 1 0 0 0 0
Mauritania 1 0 0 0 0
Mauritius 1 0 0 0 0
Mexico 0 1 0 0 0
Mongolia 0 0 1 0 0
Montenegro 0 0 0 1 0
Morocco 1 0 0 0 0
Mozambique 1 0 0 0 0
Myanmar 0 0 1 0 0
Namibia 1 0 0 0 0
Nepal 0 0 1 0 0
Netherlands 0 0 0 1 0
New Zealand 0 0 0 0 1
Nicaragua 0 1 0 0 0
Niger 1 0 0 0 0
Nigeria 1 0 0 0 0
Norway 0 0 0 1 0
Oman 0 0 1 0 0
Pakistan 0 0 1 0 0
Panama 0 1 0 0 0
Paraguay 0 1 0 0 0
Peru 0 1 0 0 0
Philippines 0 0 1 0 0
Poland 0 0 0 1 0
Portugal 0 0 0 1 0
Puerto Rico 0 1 0 0 0
Reunion 1 0 0 0 0
Romania 0 0 0 1 0
Rwanda 1 0 0 0 0
Sao Tome and Principe 1 0 0 0 0
Saudi Arabia 0 0 1 0 0
Senegal 1 0 0 0 0
Serbia 0 0 0 1 0
Sierra Leone 1 0 0 0 0
Singapore 0 0 1 0 0
Slovak Republic 0 0 0 1 0
Slovenia 0 0 0 1 0
Somalia 1 0 0 0 0
South Africa 1 0 0 0 0
Spain 0 0 0 1 0
Sri Lanka 0 0 1 0 0
Sudan 1 0 0 0 0
Swaziland 1 0 0 0 0
Sweden 0 0 0 1 0
Switzerland 0 0 0 1 0
Syria 0 0 1 0 0
Taiwan 0 0 1 0 0
Tanzania 1 0 0 0 0
Thailand 0 0 1 0 0
Togo 1 0 0 0 0
Trinidad and Tobago 0 1 0 0 0
Tunisia 1 0 0 0 0
Turkey 0 0 0 1 0
Uganda 1 0 0 0 0
United Kingdom 0 0 0 1 0
United States 0 1 0 0 0
Uruguay 0 1 0 0 0
Venezuela 0 1 0 0 0
Vietnam 0 0 1 0 0
West Bank and Gaza 0 0 1 0 0
Yemen, Rep. 0 0 1 0 0
Zambia 1 0 0 0 0
Zimbabwe 1 0 0 0 0Which leads quite naturally to the consideration of any association between the observed frequencies.
Inferential statistics
Meaningful analysis
- What is your hypothesis - what is your null hypothesis?
Always: the level of the independent variable has no effect on the level of the dependent variable.
What type of variables (data type) do you have?
What are the assumptions of the test you are using?
Interpreting the result
Testing significance
p-value
<0.05
-
0.03-0.049
- Would benefit from further testing.
0.05 is not a magic number.
Comparing means
It all starts with a hypothesis
- Null hypothesis
- “There is no difference in mean height between men and women” \[mean\_height\_men - mean\_height\_women = 0\]
- Alternate hypothesis
- “There is a difference in mean height between men and women”
More on hypothesis testing
The null hypothesis (H0) assumes that the true mean difference (μd) is equal to zero.
The two-tailed alternative hypothesis (H1) assumes that μd is not equal to zero.
The upper-tailed alternative hypothesis (H1) assumes that μd is greater than zero.
The lower-tailed alternative hypothesis (H1) assumes that μd is less than zero.
Remember: hypotheses are never about data, they are about the processes which produce the data. The value of μd is unknown. The goal of hypothesis testing is to determine the hypothesis (null or alternative) with which the data are more consistent.
Comparing means
Is there an absolute difference between the populations of European vs non-European countries?
R
gapminder %>%
group_by(european) %>%
summarise(av.popn = mean(pop, na.rm = TRUE))
OUTPUT
# A tibble: 2 × 2
european av.popn
<lgl> <dbl>
1 FALSE 32931064.
2 TRUE 17169765.Is the difference between heights statistically significant?
t-test
Assumptions of a t-test
One independent categorical variable with 2 groups and one dependent continuous variable
The dependent variable is approximately normally distributed in each group
The observations are independent of each other
For students’ original t-statistic, that the variances in both groups are more or less equal. This constraint should probably be abandoned in favour of always using a conservative test.
Doing a t-test
R
t.test(pop ~ european, data = gapminder)$statistic
OUTPUT
t
4.611907 R
t.test(pop ~ european, data = gapminder)$parameter
OUTPUT
df
1585.104 Notice that the summary()** of the test contains more data than is output by default.
Write a paragraph in markdown format reporting this test result including the t-statistic, the degrees of freedom, the confidence interval and the p-value to 4 places. To do this include your r code inline with your text, rather than in an R code chunk.
More than two levels of IV
While the t-test is sufficient where there are two levels of the IV, for situations where there are more than two, we use the ANOVA family of procedures. To show this, we will create a variable that subsets our data by per capita GDP levels. If the ANOVA result is statistically significant, we will use a post-hoc test method to do pairwise comparisons (here Tukey’s Honest Significant Differences.)
R
quantile(gapminder$gdpPercap)
OUTPUT
0% 25% 50% 75% 100%
241.1659 1202.0603 3531.8470 9325.4623 113523.1329 R
IQR(gapminder$gdpPercap)
OUTPUT
[1] 8123.402R
gapminder$gdpGroup <- cut(gapminder$gdpPercap, breaks = c(241.1659, 1202.0603, 3531.8470, 9325.4623, 113523.1329), labels = FALSE)
gapminder$gdpGroup <- factor(gapminder$gdpGroup)
anovamodel <- aov(gapminder$pop ~ gapminder$gdpGroup)
summary(anovamodel)
OUTPUT
Df Sum Sq Mean Sq F value Pr(>F)
gapminder$gdpGroup 3 1.066e+17 3.553e+16 3.163 0.0237 *
Residuals 1699 1.908e+19 1.123e+16
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1 observation deleted due to missingnessR
TukeyHSD(anovamodel)
OUTPUT
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = gapminder$pop ~ gapminder$gdpGroup)
$`gapminder$gdpGroup`
diff lwr upr p adj
2-1 -4228756 -22914519 14457007.3 0.9375254
3-1 -19586897 -38272660 -901133.5 0.0357045
4-1 -15053430 -33739193 3632332.8 0.1628242
3-2 -15358141 -34032922 3316640.4 0.1487248
4-2 -10824674 -29499456 7850106.7 0.4433887
4-3 4533466 -14141315 23208247.5 0.9243090Regression Modelling
The most common use of regression modelling is to explore the
relationship between two continuous variables, for example between
gdpPercap and lifeExp in our data. We can
first determine whether there is any significant correlation between the
values, and if there is, plot the relationship.
R
cor.test(gapminder$gdpPercap, gapminder$lifeExp)
OUTPUT
Pearson's product-moment correlation
data: gapminder$gdpPercap and gapminder$lifeExp
t = 29.658, df = 1702, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5515065 0.6141690
sample estimates:
cor
0.5837062 R
ggplot(gapminder, aes(gdpPercap, log(lifeExp))) +
geom_point() +
geom_smooth()
OUTPUT
`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'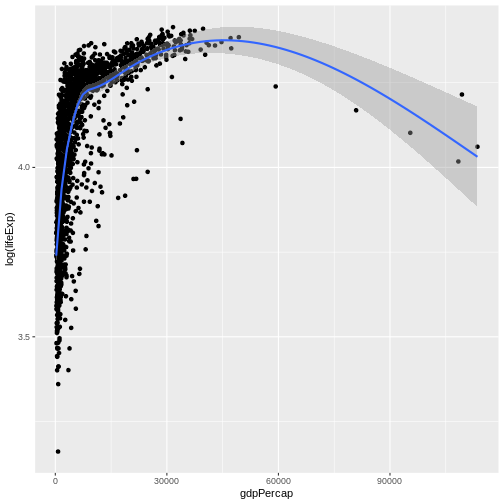
Having decided that a further investigation of this relationship is
worthwhile, we can create a linear model with the function
lm().
R
modelone <- lm(gapminder$gdpPercap ~ gapminder$lifeExp)
summary(modelone)
OUTPUT
Call:
lm(formula = gapminder$gdpPercap ~ gapminder$lifeExp)
Residuals:
Min 1Q Median 3Q Max
-11483 -4539 -1223 2482 106950
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -19277.25 914.09 -21.09 <2e-16 ***
gapminder$lifeExp 445.44 15.02 29.66 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 8006 on 1702 degrees of freedom
Multiple R-squared: 0.3407, Adjusted R-squared: 0.3403
F-statistic: 879.6 on 1 and 1702 DF, p-value: < 2.2e-16Regression with a categorical IV (the t-test)
Run the following code chunk and compare the results to the t test conducted earlier.
R
gapminder %>%
mutate(european = factor(european))
OUTPUT
# A tibble: 1,704 × 8
country continent year lifeExp pop gdpPercap european gdpGroup
<fct> <fct> <int> <dbl> <int> <dbl> <fct> <fct>
1 Afghanistan Asia 1952 28.8 8425333 779. FALSE 1
2 Afghanistan Asia 1957 30.3 9240934 821. FALSE 1
3 Afghanistan Asia 1962 32.0 10267083 853. FALSE 1
4 Afghanistan Asia 1967 34.0 11537966 836. FALSE 1
5 Afghanistan Asia 1972 36.1 13079460 740. FALSE 1
6 Afghanistan Asia 1977 38.4 14880372 786. FALSE 1
7 Afghanistan Asia 1982 39.9 12881816 978. FALSE 1
8 Afghanistan Asia 1987 40.8 13867957 852. FALSE 1
9 Afghanistan Asia 1992 41.7 16317921 649. FALSE 1
10 Afghanistan Asia 1997 41.8 22227415 635. FALSE 1
# ℹ 1,694 more rowsR
modelttest <- lm(gapminder$pop ~ gapminder$european)
summary(modelttest)
OUTPUT
Call:
lm(formula = gapminder$pop ~ gapminder$european)
Residuals:
Min 1Q Median 3Q Max
-32871053 -29780936 -22066032 -7948269 1285752032
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 32931064 2891217 11.390 <2e-16 ***
gapminder$europeanTRUE -15761300 6290196 -2.506 0.0123 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.06e+08 on 1702 degrees of freedom
Multiple R-squared: 0.003675, Adjusted R-squared: 0.00309
F-statistic: 6.278 on 1 and 1702 DF, p-value: 0.01231