Vectorization

Overview

Questions

• How can I operate on all the elements of a vector at once?

Objectives

• To understand vectorized operations in R.

Most of R’s functions are vectorized, meaning that the function will operate on all elements of a vector without needing to loop through and act on each element one at a time. This makes writing code more concise, easy to read, and less error prone.

R

x <- 1:4
x * 2

OUTPUT

[1] 2 4 6 8

The multiplication happened to each element of the vector.

We can also add two vectors together:

R

y <- 6:9
x + y

OUTPUT

[1]  7  9 11 13

Each element of x was added to its corresponding element of y:

R

x:  1  2  3  4
    +  +  +  +
y:  6  7  8  9
---------------
    7  9 11 13

Here is how we would add two vectors together using a for loop:

R

output_vector <- c()
for (i in 1:4) {
  output_vector[i] <- x[i] + y[i]
}
output_vector

OUTPUT

[1]  7  9 11 13

Compare this to the output using vectorised operations.

R

sum_xy <- x + y
sum_xy

OUTPUT

[1]  7  9 11 13

Challenge 1

Let’s try this on the pop column of the gapminder dataset.

Make a new column in the gapminder data frame that contains population in units of millions of people. Check the head or tail of the data frame to make sure it worked.

Solution to challenge 1

Let’s try this on the pop column of the gapminder dataset.

Make a new column in the gapminder data frame that contains population in units of millions of people. Check the head or tail of the data frame to make sure it worked.

R

gapminder$pop_millions <- gapminder$pop / 1e6
head(gapminder)

OUTPUT

      country year      pop continent lifeExp gdpPercap pop_millions
1 Afghanistan 1952  8425333      Asia  28.801  779.4453     8.425333
2 Afghanistan 1957  9240934      Asia  30.332  820.8530     9.240934
3 Afghanistan 1962 10267083      Asia  31.997  853.1007    10.267083
4 Afghanistan 1967 11537966      Asia  34.020  836.1971    11.537966
5 Afghanistan 1972 13079460      Asia  36.088  739.9811    13.079460
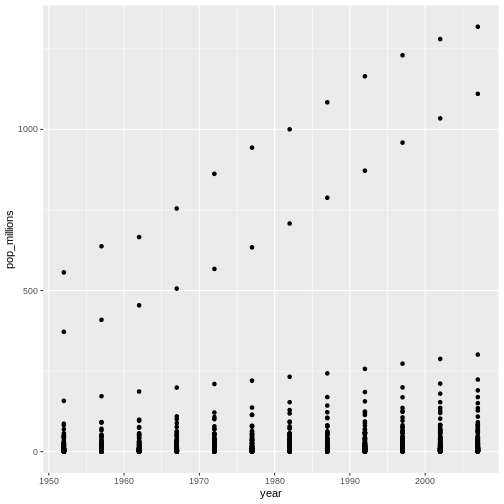
6 Afghanistan 1977 14880372      Asia  38.438  786.1134    14.880372

Challenge 2

On a single graph, plot population, in millions, against year, for all countries. Do not worry about identifying which country is which.

Repeat the exercise, graphing only for China, India, and Indonesia. Again, do not worry about which is which.

Solution to challenge 2

Refresh your plotting skills by plotting population in millions against year.

R

ggplot(gapminder, aes(x = year, y = pop_millions)) +
 geom_point()

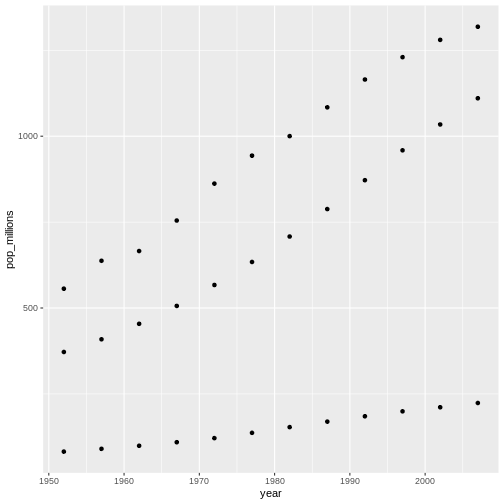
R

countryset <- c("China","India","Indonesia")
ggplot(gapminder[gapminder$country %in% countryset,],
       aes(x = year, y = pop_millions)) +
  geom_point()

Comparison operators, logical operators, and many functions are also vectorized:

Comparison operators

R

x > 2

OUTPUT

[1] FALSE FALSE  TRUE  TRUE

Logical operators

R

a <- x > 3  # or, for clarity, a <- (x > 3)
a

OUTPUT

[1] FALSE FALSE FALSE  TRUE

Tip: some useful functions for logical vectors

any() will return TRUE if any element of a vector is TRUE.
all() will return TRUE if all elements of a vector are TRUE.

Most functions also operate element-wise on vectors:

Functions

R

x <- 1:4
log(x)

OUTPUT

[1] 0.0000000 0.6931472 1.0986123 1.3862944

Vectorized operations work element-wise on matrices:

R

m <- matrix(1:12, nrow=3, ncol=4)
m * -1

OUTPUT

     [,1] [,2] [,3] [,4]
[1,]   -1   -4   -7  -10
[2,]   -2   -5   -8  -11
[3,]   -3   -6   -9  -12

Tip: element-wise vs. matrix multiplication

Very important: the operator * gives you element-wise multiplication! To do matrix multiplication, we need to use the %*% operator:

R

m %*% matrix(1, nrow=4, ncol=1)

OUTPUT

     [,1]
[1,]   22
[2,]   26
[3,]   30

R

matrix(1:4, nrow=1) %*% matrix(1:4, ncol=1)

OUTPUT

     [,1]
[1,]   30

For more on matrix algebra, see the Quick-R reference guide

Challenge 3

Given the following matrix:

R

m <- matrix(1:12, nrow=3, ncol=4)
m

OUTPUT

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Write down what you think will happen when you run:

1. m ^ -1
2. m * c(1, 0, -1)
3. m > c(0, 20)
4. m * c(1, 0, -1, 2)

Did you get the output you expected? If not, ask a helper!

Solution to challenge 3

Given the following matrix:

R

m <- matrix(1:12, nrow=3, ncol=4)
m

OUTPUT

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Write down what you think will happen when you run:

1. m ^ -1

OUTPUT

          [,1]      [,2]      [,3]       [,4]
[1,] 1.0000000 0.2500000 0.1428571 0.10000000
[2,] 0.5000000 0.2000000 0.1250000 0.09090909
[3,] 0.3333333 0.1666667 0.1111111 0.08333333

2. m * c(1, 0, -1)

OUTPUT

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    0    0    0    0
[3,]   -3   -6   -9  -12

3. m > c(0, 20)

OUTPUT

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE FALSE  TRUE FALSE
[2,] FALSE  TRUE FALSE  TRUE
[3,]  TRUE FALSE  TRUE FALSE

Challenge 4

We’re interested in looking at the sum of the following sequence of fractions:

R

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

This would be tedious to type out, and impossible for high values of n. Use vectorisation to compute x when n=100. What is the sum when n=10,000?

Challenge 4

We’re interested in looking at the sum of the following sequence of fractions:

R

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

This would be tedious to type out, and impossible for high values of n. Can you use vectorisation to compute x, when n=100? How about when n=10,000?

R

sum(1/(1:100)^2)

OUTPUT

[1] 1.634984

R

sum(1/(1:1e04)^2)

OUTPUT

[1] 1.644834

R

n <- 10000
sum(1/(1:n)^2)

OUTPUT

[1] 1.644834

We can also obtain the same results using a function:

R

inverse_sum_of_squares <- function(n) {
  sum(1/(1:n)^2)
}
inverse_sum_of_squares(100)

OUTPUT

[1] 1.634984

R

inverse_sum_of_squares(10000)

OUTPUT

[1] 1.644834

R

n <- 10000
inverse_sum_of_squares(n)

OUTPUT

[1] 1.644834

Tip: Operations on vectors of unequal length

Operations can also be performed on vectors of unequal length, through a process known as recycling. This process automatically repeats the smaller vector until it matches the length of the larger vector. R will provide a warning if the larger vector is not a multiple of the smaller vector.

R

x <- c(1, 2, 3)
y <- c(1, 2, 3, 4, 5, 6, 7)
x + y

WARNING

Warning in x + y: longer object length is not a multiple of shorter object
length

OUTPUT

[1] 2 4 6 5 7 9 8

Vector x was recycled to match the length of vector y

R

x:  1  2  3  1  2  3  1
    +  +  +  +  +  +  +
y:  1  2  3  4  5  6  7
-----------------------
    2  4  6  5  7  9  8

Key Points

• Use vectorized operations instead of loops.