Introduction to Zacros

Zacros:

• Kinetic Monte Carlo (KMC) simulation of surface chemistry
• Graph theoretical framework
  • Handle complex surface patterns

For more info visit: zacros.org

Reaction patterns

• Possible reactions get a time assigned based on:
  • kinetic rate constants (Propensities)
  • A random number

See Stamatakis and Vlachos. 2011. J. Chem. Phys. 134(21): 214115 and Nielsen et. al. 2013. J. Chem. Phys. 139(22): 224706

Surface energy

To calculate rates, the surface energy is needed:

• Surface energy is given as a cluster expansion
• I.e. an expansion in simple surface patterns

Pseudo code

• Select most imminent process
• Remove adsorbates from lattice
• Remove clusters with reactants
• Remove reactions involving the reactants
• Add product adsorbates
• Find new energy clusters
• Find existing processes that need update
• Update rates of existing processes
• Add new processes

Technical

• Fortran 95/2003 code
• Originally fully serial
• Two performance issues with serial code identified

Cluster Expansion

• Long range interactions requires large cluster expansions
• Larger cluster expansions => More processes to update
• This is the first performance issue

Lattice size

Large lattice for accurate simulations

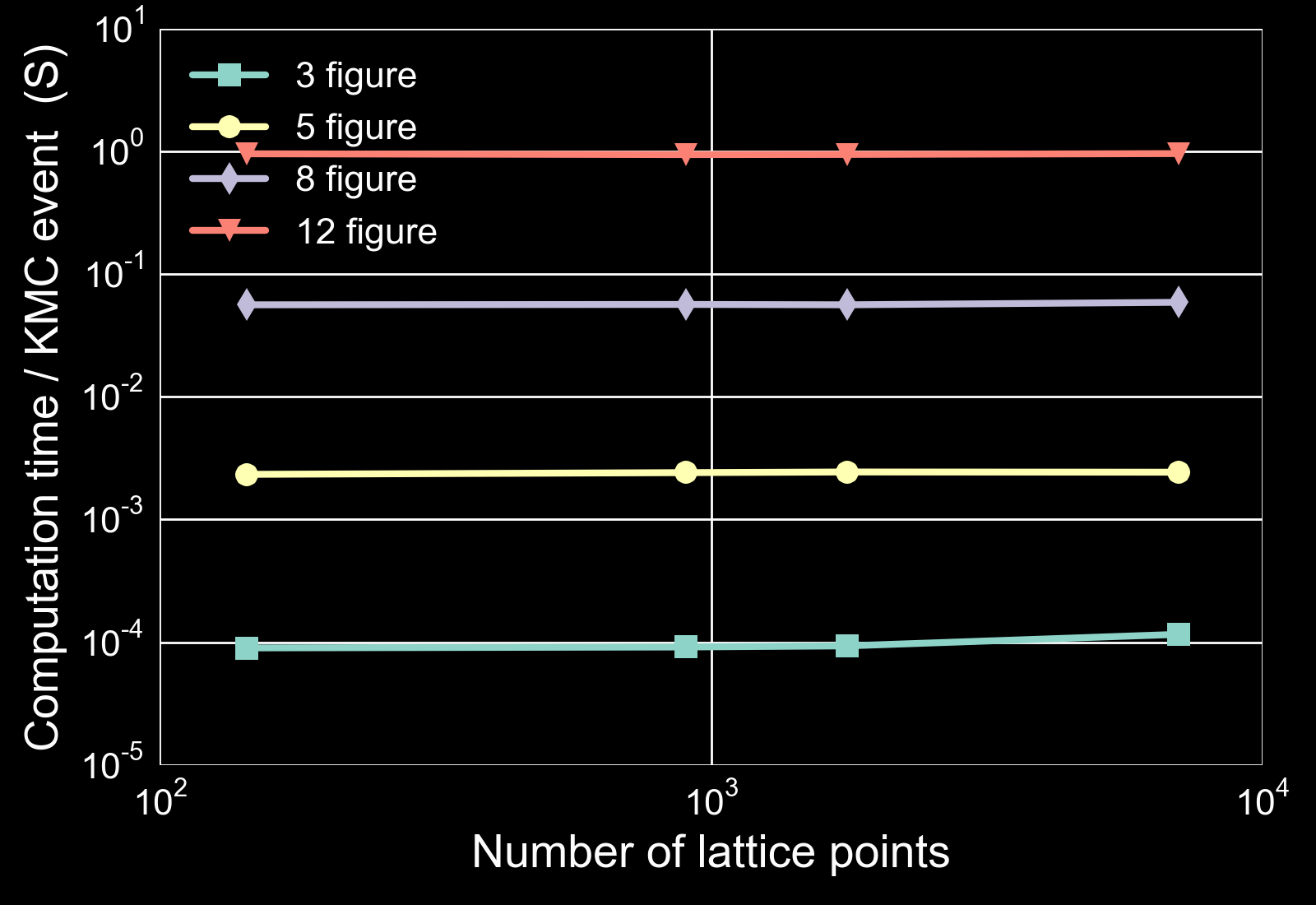
• Update time is independent of lattice size
• But reaction rate is not
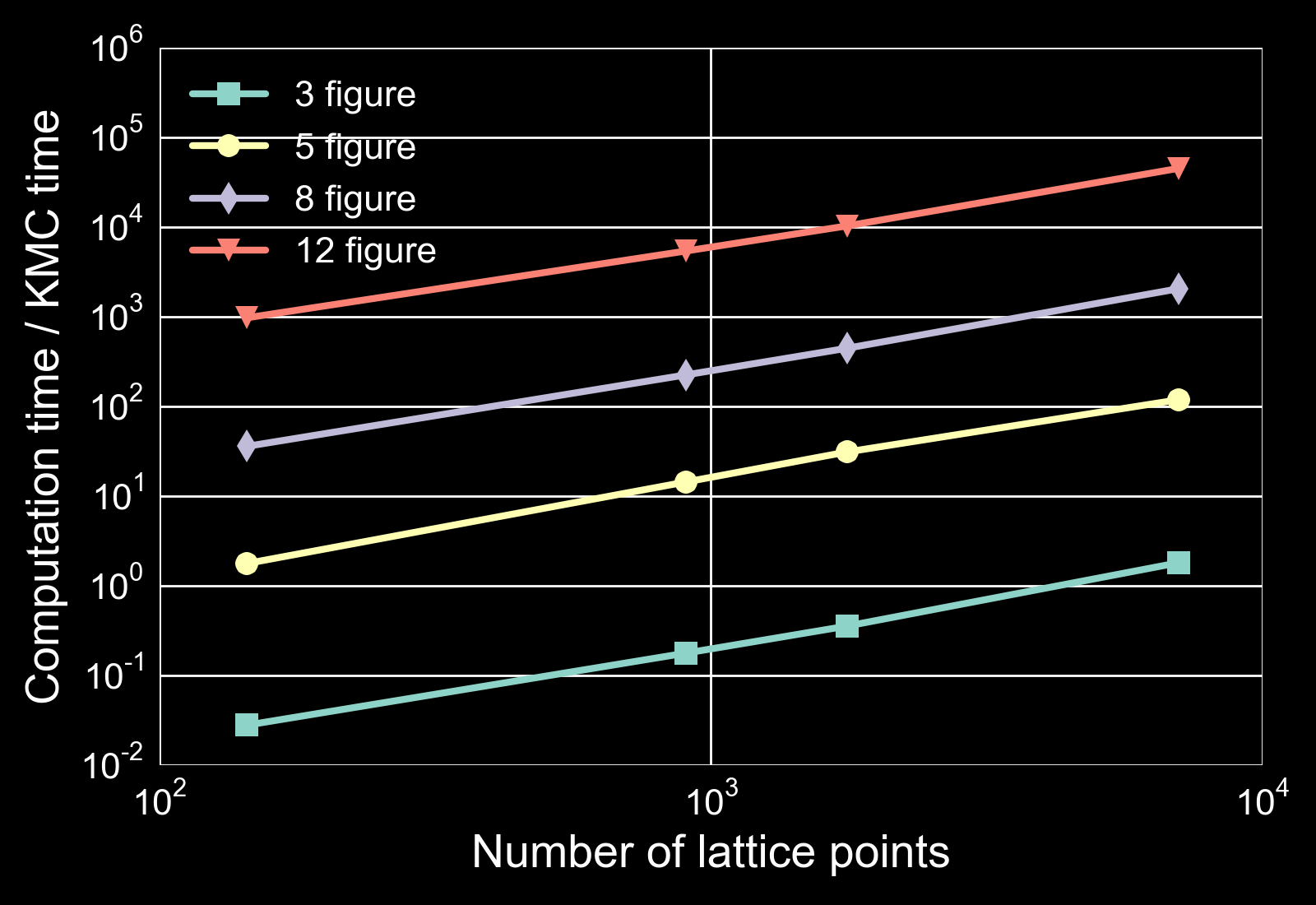
• KMC time / CPU time depends linearly on the number of sites
• Large lattices are time consuming to simulate
• The second performance issue

Reaction updates:

OpenMP:

• Profiling shows bottleneck in update rates ...
• Many processes are affected
  • Especially for large cluster expansion
• Do loop of independent processes to update
• OpenMP parallization of this loop

See Nielsen et. al. 2013. J. Chem. Phys. 139(22): 224706

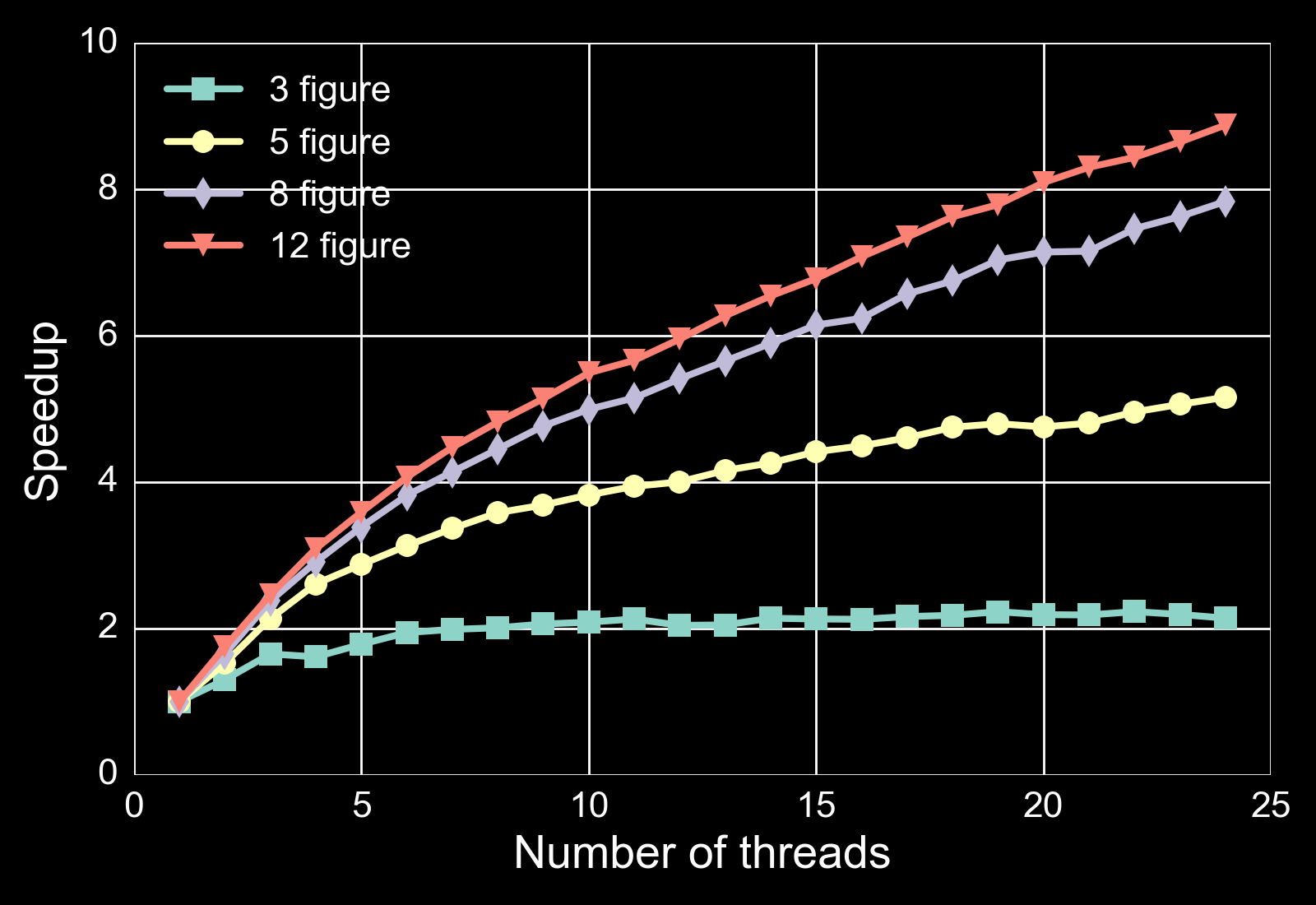
Scaled performance of OpenMP

Computational time per event

Computational time / KMC time

• But number of events per simulated second is not
• 12 figure expansion at 7056 lattice points (12 threads):
  • $> 10^4$ seconds per simulated second

Limitations

Decent speed up for large cluster expansions but:

• OpenMP limited to one computational node
• Simulations are still too slow for large lattices and clusters

Solution: MPI Parallelization over lattice

Spatial Parallelization

MPI based parallelization

• Reactions on individual domains
• Halo for
  • Reactants
  • Products
  • Energetic clusters

Original plan:

Implement algorithm proposed by Lubachevsky

• Algorithm is developed for Ising spin model
• Each domain keeps track of a local time
• Global time is min(localTimes)
• Updates in a MPI domain is allowed if:
  • Local time is smaller than all neighbours

Lubachevsky. 1988. J. Comp. Phys. 75 (1): 103

Algorithm

• Perform spin flip if time is smallest among neighbours
• Select a site and either:
  • Perform spin flip
  • Perform null event
• Advance local time by a random interval
• Repeat

Time advancement is independent of whether a spin is flipped

Energetics affect the relative probability of null events

Algorithm in Zacros

Same principle:

• If local time < neighbours time:
  • Advance local time
  • Perform reaction
  • Send halo and new local time
• Else:
  • Wait to receive halo and time

Issues in Zacros

• Future reactions have a wait time associated with them
• Wait time is random but determined by reaction rates
• Most imminent reaction is performed
• Reaction happen after wait time
• Wait time can differ by several orders of magnitude

Example

Assume that we have 3 MPI nodes in a 1D array

Both $P1$ and $P3$ are free to perform reactions

Example

Assume that we have 3 MPI nodes in a 1D array

Conflict $\textrm{P}_1$ should not have performed a reaction

In summary

• Can't change the condition to smallest among $T{local} + T{wait}$
  • The reactions that $T_{wait}$ on neighbours represent have not happened:
  • In fact they may never happen
  • Reactions may propagate across domains

Alternative strategies

An alternative proposed by Jefferson

• Each node propagates its reactions without synchronization
• Stores a list of anti reactions to performed reactions
• When a reaction is performed messages are sent to relevant neighbours

Jefferson. 1985. ACM Trans. Program. Lang. Syst. 7 (3): 404

Alternative strategies

• If conflicts arise neighbours will roll-back
  • Sending anti messages to their neighbours
  • With further potential roll-back
• The "slowest" node determine a virtual time horizon (Global time)
  • No roll-backs beyond this the are needed

Conclusion

Conclusion

• Good performance improvement for long range interactions
• Spatial parallelization is on-going work
  • Change of algorithm